3D trace elements-- how does the internal standardization calculation work?

edmarshall

I would like to use the 3D Trace Elements DRS, as it seems to outperform the older Longerich et al. (1996)-based trace elements DRS, but I'm having trouble understanding how the new data reduction scheme works. Maybe this is a good venue to ask this question.

In Paul et al. (2023), which describes the 3D trace elements approach, the first step of calculations seems to be creating a calibration curve for each standard block, concentration against intensity, and then extrapolating the calibration curves between the blocks to cover the sample data. The paper also seems to describe the older Longerich-based calculation method as a "single point calibration curve". As you all know well, laser ICPMS data doesn't work well with calibration curves because of drift, changes in laser settings between spots, matrix effects between phases, etc. The Longerich-approach sidesteps calibration curves by using internal standardization, so it is confusing to me that it is described as a "single point calibration curve", and thus very confusing to me that the 3D trace elements data reduction scheme is described as a multi-reference material calibration curve that is extrapolated through time. How does it actually work? How does internal standardization work with this approach?

Is there somewhere where the calculation procedure is explicitly written out? Thanks for your help!

Bence

Hi @edmarshall

This a good question. I started writing a reply here but it started to get a bit long. So I've turned it into a blog post:

https://notes.iolite.xyz/posts/tes_combined/

If you have any questions after reading that, or if you spot any errors, please feel free to post here.

Kind regards,
Bence

edmarshall

Thanks so much for answering this question. After posting it, I had decided that the question was too onerous, and had deleted it and started working through the DRS code myself. This has been slow going and I really appreciate you dredging it back up and answering it fully.

I guess a point of confusion was that the calculation process is described as a two step process. The code does work this way, so it's certainly accurate to describe it this way. But let me try to describe it as if it were a single step process, and see if this is correct:

The Longerich equation is (using the variable names from your blog post):

And because sensitivity is defined:

Then, by substitution we could rewrite the Longerich equation to be:

Within this way of thinking about it, the biggest difference between the older Trace Elements approach and the new 3D Trace Elements approach is that the sensitivities for the RMs are calculated very differently. In the old trace elements DRS they were calculated from measurements of a single RM, and then (if I understand correctly) the sensitivities at each time point are given by a chosen function (spline, linear fit, mean, whatever). However, in the new 3D trace elements DRS, the sensitivities are produced from linear concentration-intensity fits of each block of standard data (if the fits are forced through zero, then the sensitivity is the slope of the fit line). These fits are then extrapolated through time (using splines, linear fit, mean, whatever) allowing sensitivity to be calculated from the fits at each time point.

So unless I messed up somewhere, this means that essentially the 3D trace elements DRS is creating sensitivities for each element by averaging together (well not really averaging, fitting is not averaging-- but not sure what to call it) the sensitivities of several different standards. This is a super cool way to do it!

Thanks again!

BTW-- some equations in your blog post are a bit messed up on my end. Here's what I see (tried in Chrome and in Edge):

Bence

edmarshall I really appreciate you dredging it back up and answering it fully.

Not a problem! We are very keen to ensure that iolite is not a "black box" and that interested and inquisitive folks such as yourself can really drill down into what iolite is doing. And if you find an error, or a better way of doing it, we can incorporate those changes and make iolite better in the process 😃

I would agree with the equation you show for Li, which is just the count rate of the sample divided by the sensitivity of the RM (this is the same as dividing by the slope in the more traditional calibration curve approach), and then multiplying this by a sensitivity ratio for the Int stds between the RM and the sample. I would just rearrange it to:

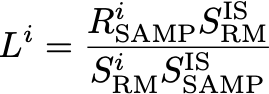
to make it clear that you're dividing the count-rate by the sensitivity and then multiplying that by a correction factor... but it's exactly the same as the way you put it.

edmarshall In the old trace elements DRS they were calculated from measurements of a single RM, and then (if I understand correctly) the sensitivities at each time point are given by a chosen function (spline, linear fit, mean, whatever).

Yes, this is correct.

edmarshall in the new 3D trace elements DRS, the sensitivities are produced from linear concentration-intensity fits of each block of standard data (if the fits are forced through zero, then the sensitivity is the slope of the fit line).

You are correct that the sensitivity is the slope of the fit to the RMs, but this is always the case whether the fit is forced through zero or not. Remember sensitivity is just the slope of the line in the tradtional calibration curve plot: steeper line means better sensitivity and vice versa. I tend to avoid the confusion between "sensitivity = slope of calibration plot line" vs "sensitivity = R / c" by referring to the latter as "yield". They're the same if you assume zero intercept and use a single RM, but if you're using a fit to multiple RMs, it's the slope of that line.

edmarshall These fits are then extrapolated through time (using splines, linear fit, mean, whatever) allowing sensitivity to be calculated from the fits at each time point.

💯 We interpolate the slope and intercept of the calibration plot so that at any point in time you could reconstruct an interpolated calibration plot.

edmarshall this means that essentially the 3D trace elements DRS is creating sensitivities for each element by averaging together (well not really averaging, fitting is not averaging-- but not sure what to call it) the sensitivities of several different standards. This is a super cool way to do it!

Yes, exactly. Fitting a line to multiple RMs is what I would describe it as.

The only wrinkle in this approach that is (slightly?) ignored by previous attempts at multi-RM calibration for LA-ICP-MS is that your calibration curve may be affected by the different ablation properties of your RMs. For example, if you use NIST glasses and basalt glasses, as we did in our paper, you can see very slight differences in the yield of each. There's a yield correction built into the calibration curve where you select a primary RM and then all the other RMs yields are adjusted relative to that, but it might not be necessary if you're using all the same matrix type RMs and discussing that correction could perhaps be another post by itself!

Thanks for asking probing questions, and thanks for the heads up about the equations in the Note.

Bence